机器学习

0x01 机器学习的定义及任务

1.定义

machine learning本质上是一个function，但是这个function过于复杂所以人类无法使用明确的函数表达式表达出来，于是将输入数据输入到计算机中，让计算机通过学习拟合出一个function来，这样就可以通过该function来预测给定输入的输出值。这个过程就是机器学习的过程。

2.机器学习的任务/分类

既然机器学习的目的是找出一个function来预测输出，那么根据输出数据的特征，就可以把机器学习分为几个类别。

• regression也叫做回归。也就是一个输入变量为N为的向量，输出是一维的scalar的一个函数。
• classification称之为分类。也就是结果为指定的某几个值，函数的输出为在这几个值中选择最可能的作为输出。比如常见的判断真假对错是否的二分类，手写数字识别的十分类，甚至是19*19=361的围棋预测。
• structured也就是生成式机器学习，在近几年流行起来的机器学习类别。

0x02 如何找出function

在这一章中我们考虑回归算法的机器学习，也就是输出y为标量值。

1.构造function的结构

首先先构造或者说确定好带有未知参数的function的结构，这些未知参数就是需要机器学习的内容。这个带有未知参数的function就称之为model，

例如定义:

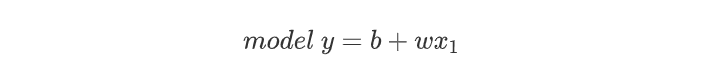
可以看出，参数的选取，例如本例中的b和w的选值将直接决定输出（也就是预测结果）的好坏。，那么该如何选取参数的值，以确保有一个好的预测结果呢？这就需要用到损失函数Loss

2.定义损失函数Loss

损失函数实际上也是一个函数，这个函数的输入为model的参数值，输出表示为当前所选取的参数的优秀程度，如可以写为L(b,w)

损失函数的输出值应该从训练数据中得到，根据模型的预测值与实际值之间的误差大小来判断当前参数的“优秀”程度。比如我们考虑上面例子中最简单的线性函数，假设训练数据为100组x与y的值，我们的Loss函数选用最简单的均值绝对值误差mean absolute error（MAE）。

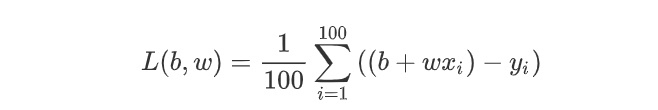
得到输出值为预测数据与训练数据的均值误差。L越小说明拟合的效果越好。常见的L还可以选取mean square error（MSE）

常用的损失函数：

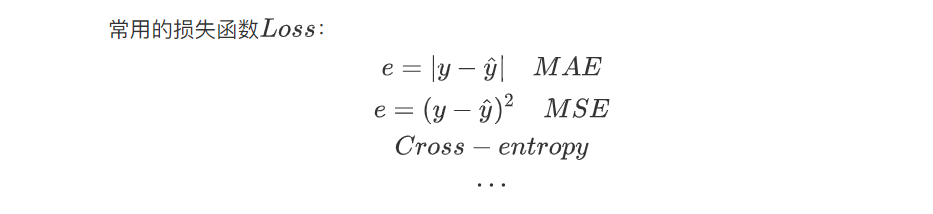
3.Optimization

当我们确定了loss之后，我们就可以对model选用不同的参数，来评估不同参数的优秀程度，所以接下来我们要做的事情就是找出参数的最优解，从而得到model的最佳拟合。

即：

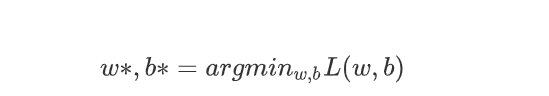
具体的求解方法可以参考《最优化原理与方法》课程中的学习内容，但是在实践中最为常用的方法一般是梯度下降法(Gradient Descent)

具体一点就是如下的步骤

• 首先选取一个初始点，设z = [b,w],求取z的最优解。

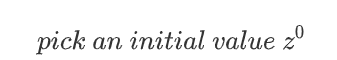
• 然后计算该点的梯度。

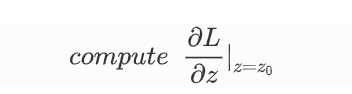
• 为了控制步长，我们需要引进一个参数η，以确保下降过程不会出现锯齿或者收敛过慢。这个引入的参数η称之为学习率（Learning rate），是一个需要手动设置的参数，在机器学习中，这样的参数叫做超参数(Hyperparameter)

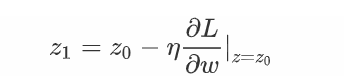
• 更新z的值，重复迭代直到指定次数或者指定精度。

4.完善function

通过上述的步骤我们了解了一个机器学习训练出function的基本过程，上述例子中我们选取的是单一变量x1，参数也只有b和w1，这样的模型显然太简单了，下下面我们推广到更高维的线性模型。实际上也只是大同小异，在前面的基础上将scalar变成victor而已。

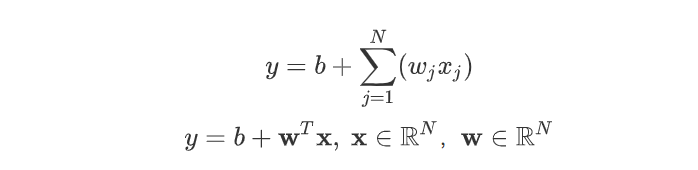
然后将Loss函数也改写为victor的形式

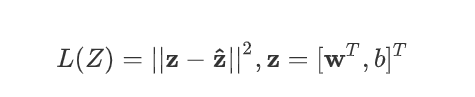
这样我们就能够实现任意维度输入的线性回归function求解了。

0x03 深度学习基本概念

1.sigmoid模型的建立

线性model的结构太过于简单，他只能对于整体的趋势进行一个唯一斜率的线性拟合，但是可能输入数据之间会呈现斜率的突然变化，如下图所示的情况，这个时候线性模型无论如何调整都无法实现较好的拟合效果，这种来自模型本身的偏差称之为Model Bias

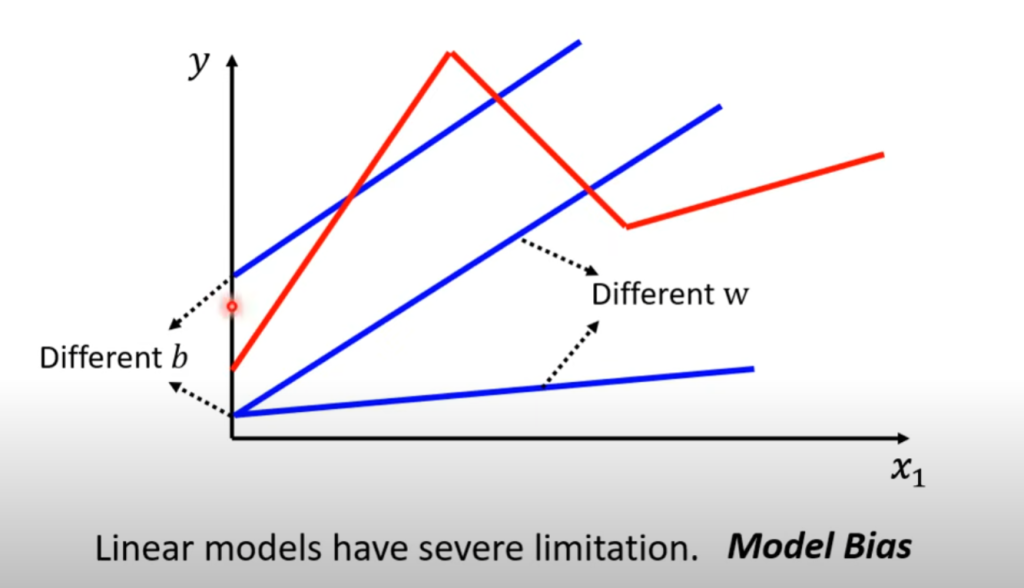
这个时候我们就需要more sophisticated的模型。

我们知道所有复杂的曲线我们都可以使用折线来进行拟合，对于上面红色线条，我们可以将其分成三段，使用三个不同的折线来拟合，这样就能解决问题了。但是所以的折线都应该有一个统一的函数表达式，这样才能简化计算过程。

我们将这样的折线通通使用如下的线段来表示：

称之为hard sigmoid函数，显然这是一个理想的模型，实际的sigmoid函数其数学表达式为

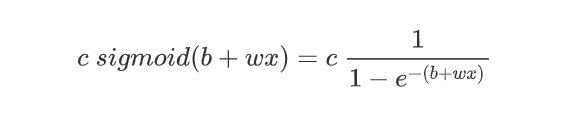
如下图所示：

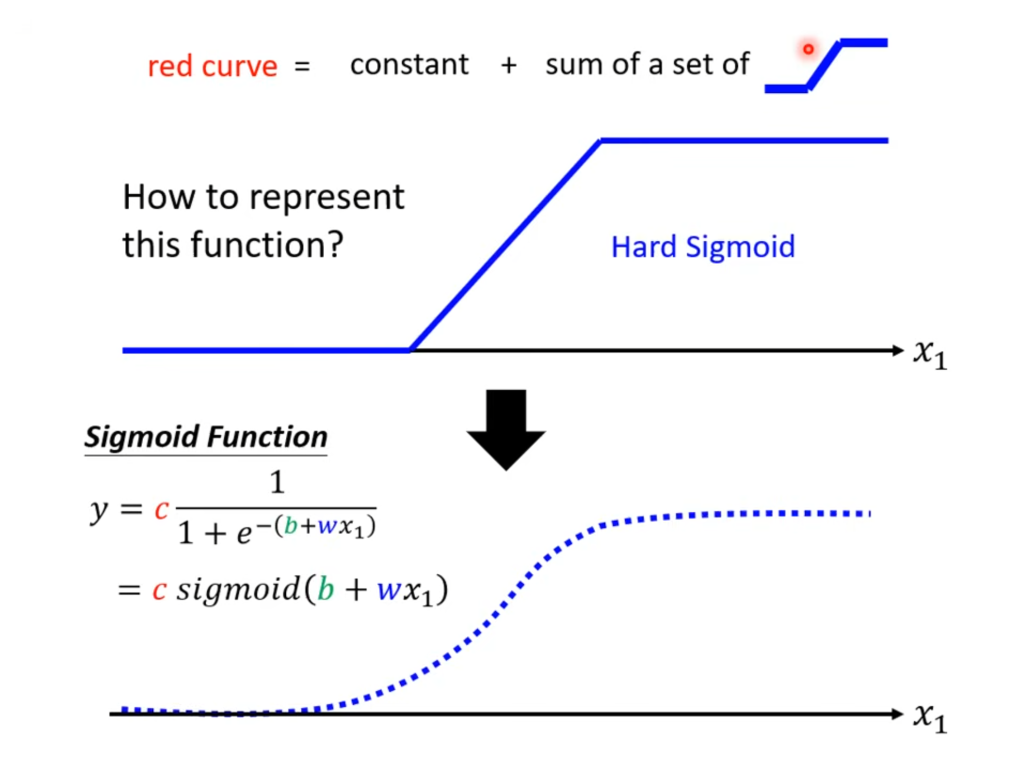
当x小如下于x1的时候，y趋近于0，当x大于x1的时候，y将趋近于c，所以我们可以通过调节c,b,w来实现不同的折线化图形。如下图所示

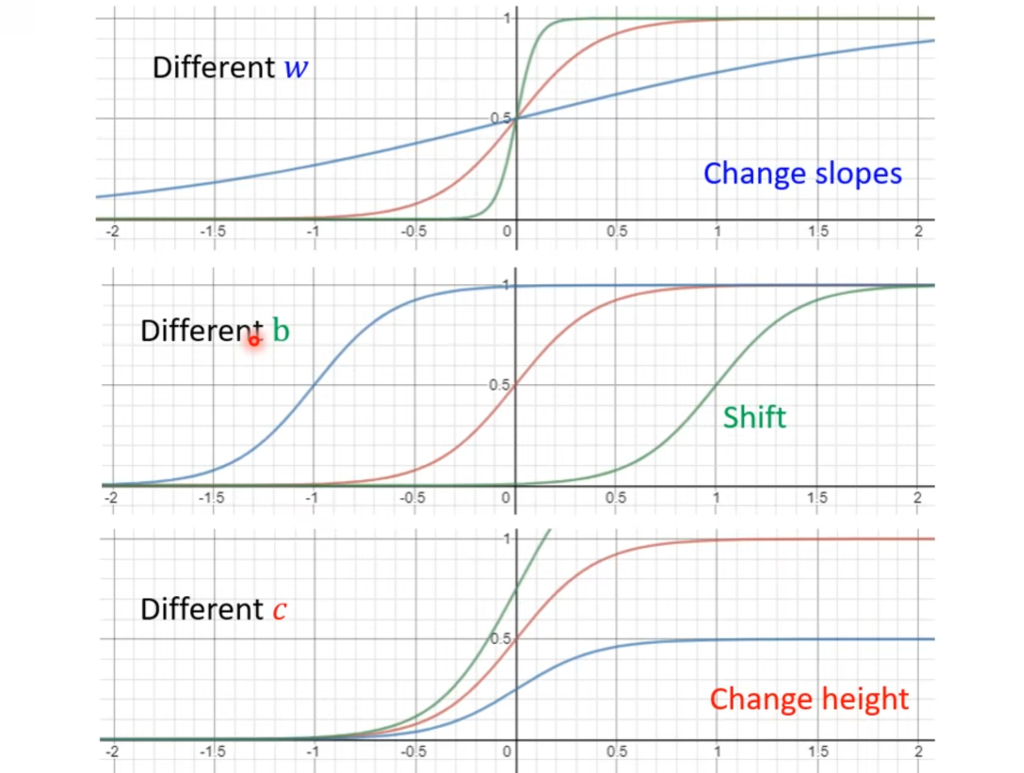
所以只要我们选取的点足够多或者选得恰当，我们就可以使用一系列的sigmoid函数就可以拟合出任意形状的曲线。同样，选取的sigmoid函数数量也是一个hyperparameter

同样，我们拓展到向量的形式。

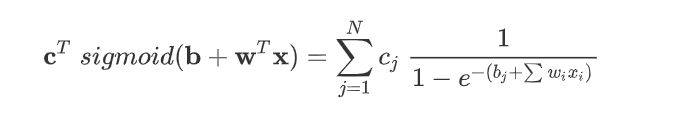
再加上常量b得到model的表达式

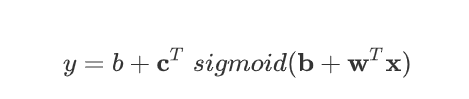
得到了sigmoid模型的表达式了之后，我们接下来看看Loss函数是否会发生改变。

我们将模型中待定的参数b,b,w,c,组合为待求参数向量θ，于是

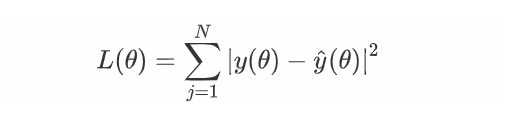
与线性模型并无明显变化，同样求最优解也无明显变化，这里不再赘述。

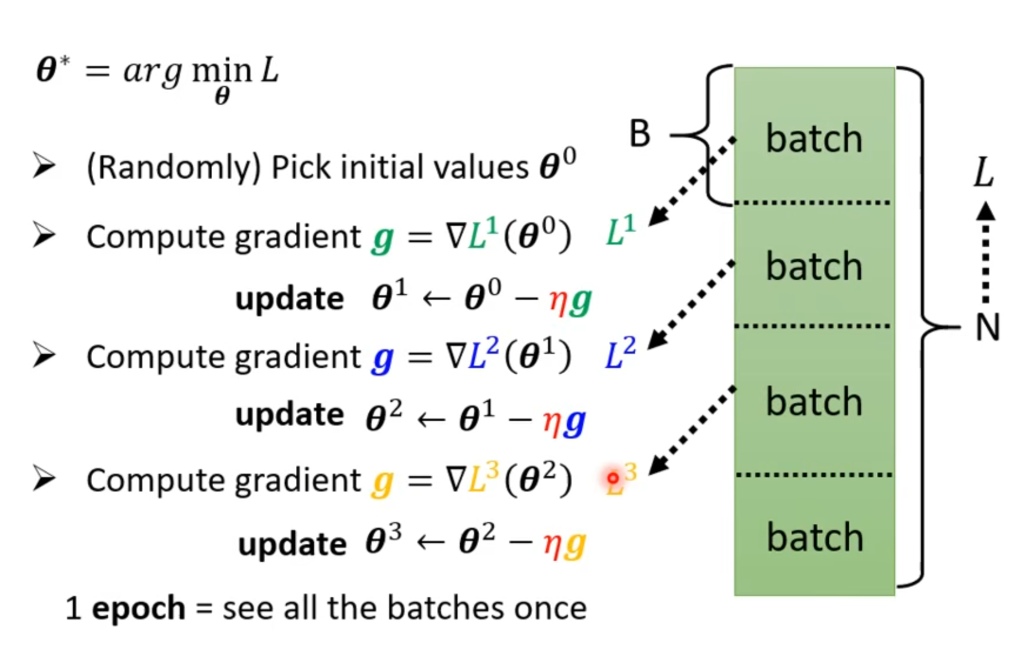
在这里同时引入一些深度学习的概念。我们可以发现，虽然模型的拟合效果变好了，但是代价是待定参数的维度增加了很多倍，因此如果Loss仍然将全部的训练数据作为输入的话会使得训练时间大大增加，如果训练数据集很大，我们可以将其划分为多个样本，用每一个样本计算出的Loss值来代替该参数在全部数据中的Loss值，在样本划分得当的情况下二者相差不会太大，但是训练速度能大大提高。因此我们将每一个划分的样本称为一个batch,每次训练完1 batch就更新一次参数，称之为(update),每训练完一轮所有的batch成为完成1 epoch的训练。如下图所示：

2.从sigmoid到ReLU

我们可以看到上面使用到的sigmoid函数实际上是soft sigmoid，只是对hard sigmoid的一个近似，那能不能直接使用hard sigmoid来实现呢？接下来引出ReLU函数。

rectified linear unit(ReLU) function：

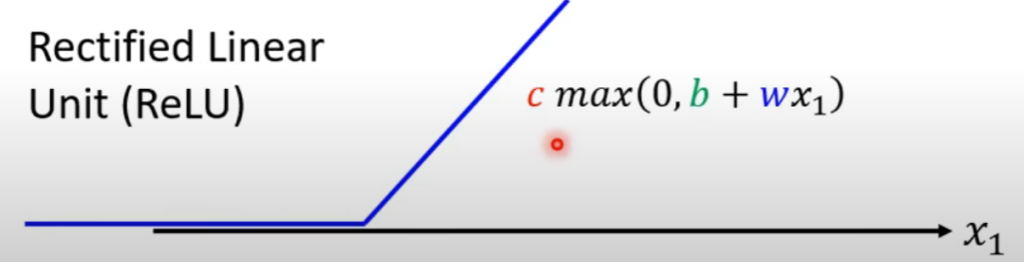
图像如上图所示，使用两个ReLU函数组合，即可绘制出一个hard sigmoid函数。

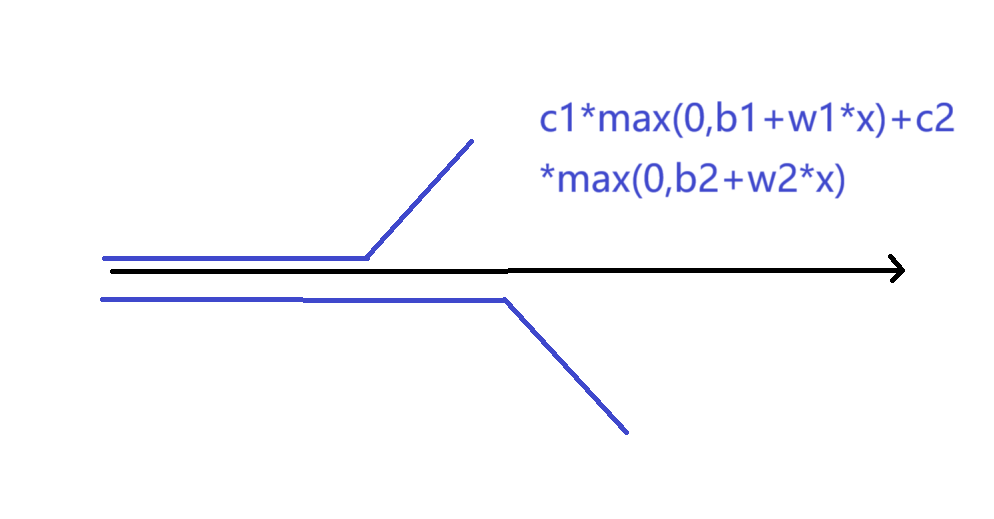
从而我们得到了hard sigmoid的一种表达式，我们使用ReLU函数来作为function，实现机器学习，从而能得到更好的预测效果。

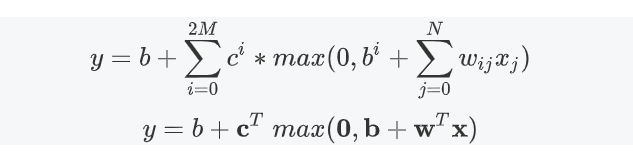
不论是sigmoid函数还是ReLU函数，在机器学习中，我们都称之为activation function

思考题：为什么ReLU函数作为function能得到更好的预测效果？

3.从单层神经网络到deep learning

上述我们讨论的都是从输入经过一个function之后直接得到输出。但是我们也可以将每一个函数的输出作为下一个函数的输入，多次计算得到最后的输出。如图所示：

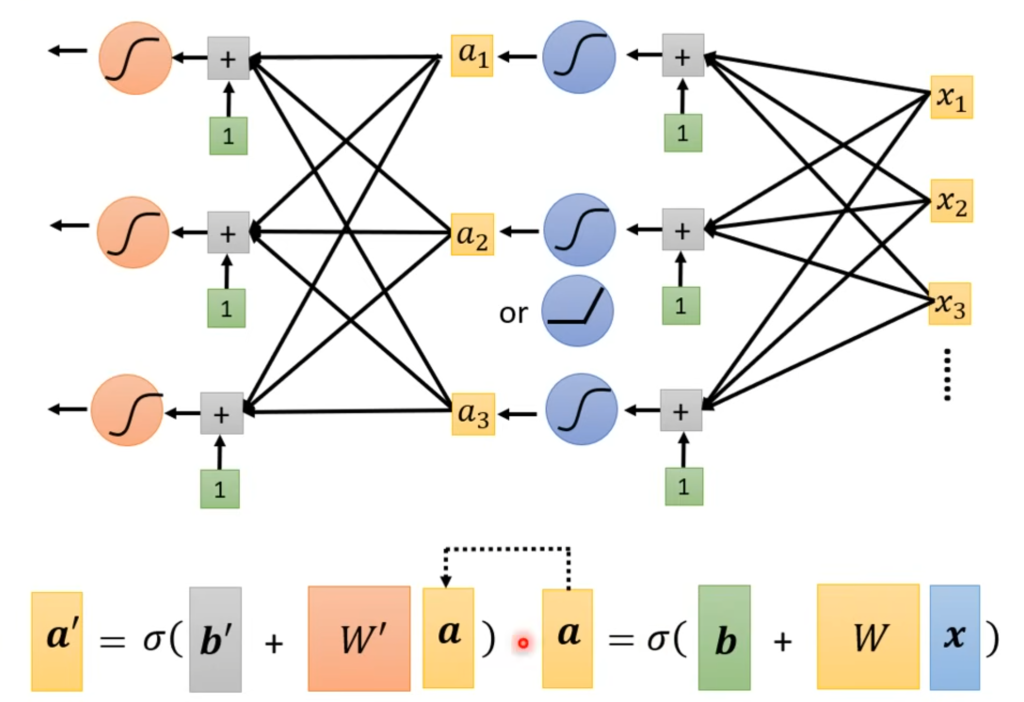
这样我们使用了多组函数来进行计算，最后得到输出值。这次过程中：

• 每一个函数结点称之为：一个神经元（neuron）。
• 每一组使用了相同输入的神经元组成了：一层（layer）。由输入作为变量的第一层称之为输入层，也叫感知层，结果作为输出的最后一层称之为输出层。其余的称之为中间层，也称之为隐藏层。
• 整个从输入到输出的部分就称之为：神经网络（neural network），也称之为类神经网络。

从上个世纪八十年代开始，神经网络的出现和发展，中间层的规模不断壮大，从AlexNet（2012）的8 layers 到AGG(2014) 的 19 layers 再到后来的Residual Net（2015）的152 layers。中间层的设计越来越复杂。使得整个神经网络变得十分复杂，也变得更加“深”，所以这样的神经网络也就被赋予了一个新的名字deep learning

过拟合现象（overfitting）:并不是隐藏层的层数越多越好，随着层数的增加，预测结果会出现对训练数据呈现出很好的拟合效果，但是预测数据的误差变大，这样的现象称之为过拟合现象。

思考题：我们知道，只要选取的ReLU函数数量足够多，就可以拟合出任意复杂的曲线，也就是说只要神经元的数量足够多就可以实现很好的拟合效果，那么为什么神经网络的发展没有朝着单层但是更多神经元的方向fat发展，而是出现了多层，朝着deep的方向发展了呢？

4.机器学习任务指南

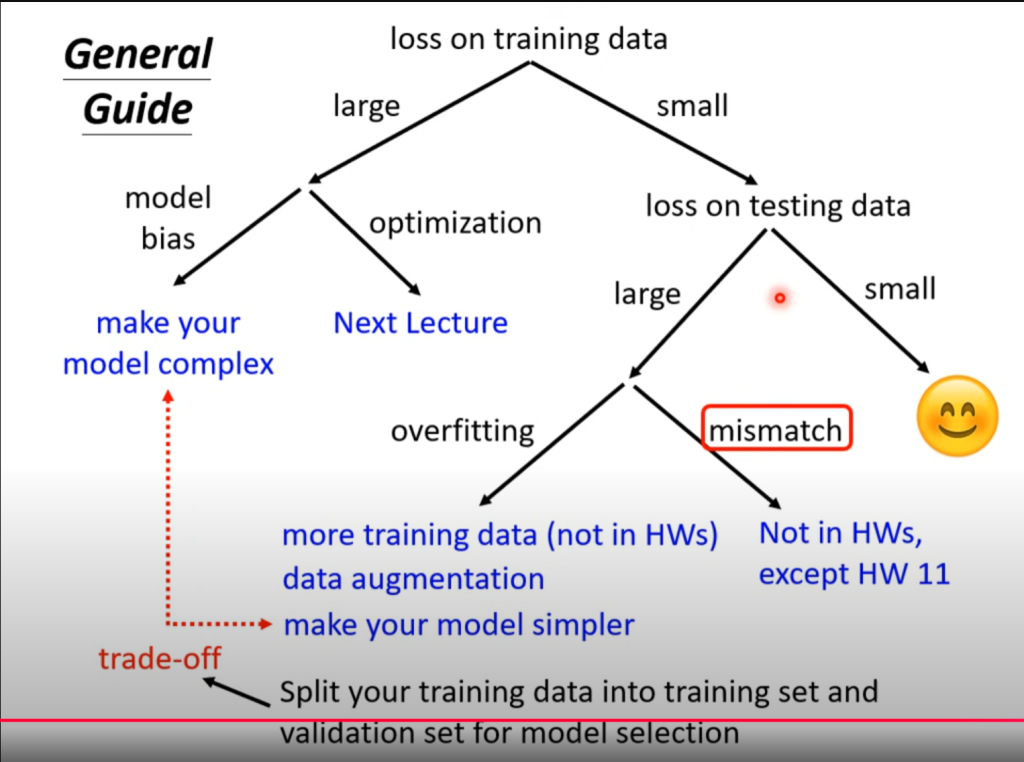
overfitting的出现：

• 因为数据集本身具有随机性，比如

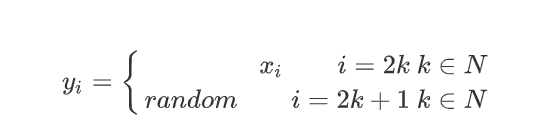
• 上面的函数式即使模型在训练数据集中表现出很好的拟合，但是对于测试数据集，由于奇数为不确定的，所以不会有很好的拟合效果。
• 训练数据集过小，导致在没有训练数据集的区间存在freestyle，模型预测数据会很大，如下图所示：

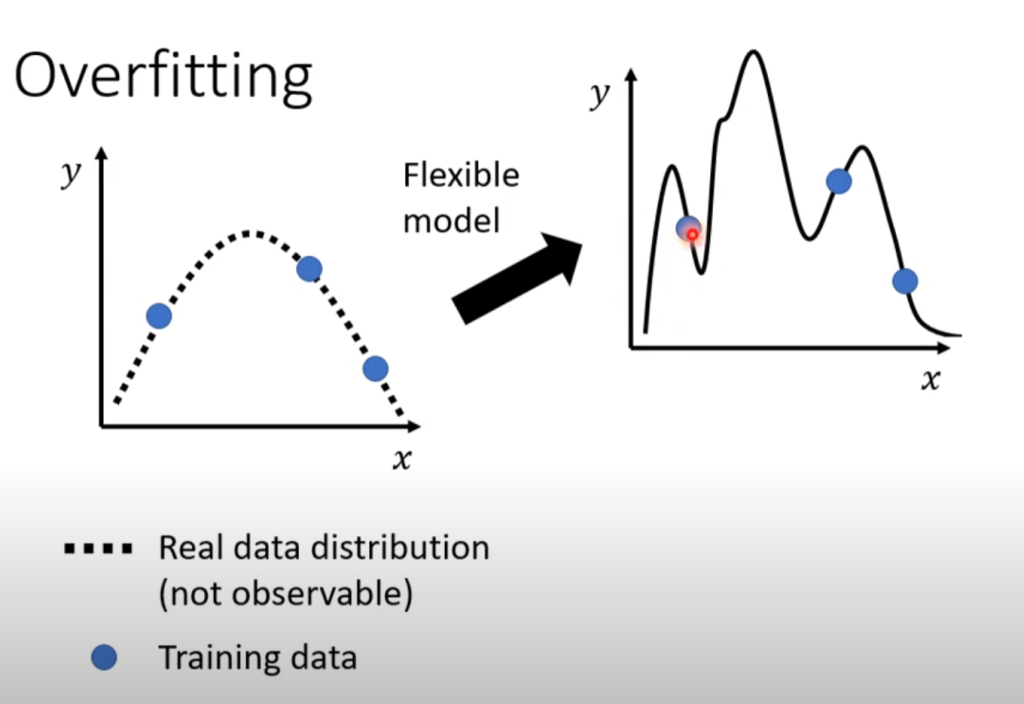
对于这种情况，可以增加数据集，或者根据数据的特点选取对应的模型，比如上图所示的数据明显符合二次曲线，所以就可以选取

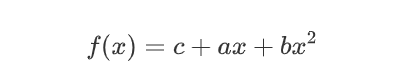
通过调整模型，也可以有很好的效果。

0x04 类神经网络训练问题

1.局部最小点与鞍点

我们知道，我们可以用泰勒展开来拟合函数在某点附近的函数表达式：

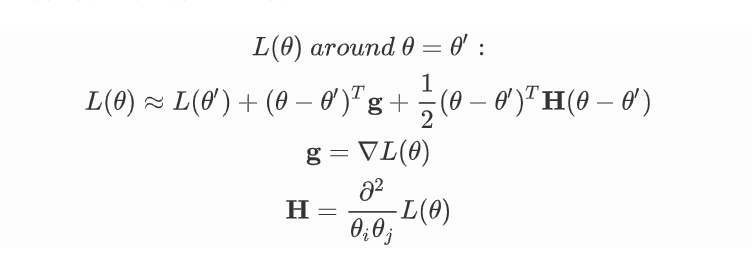
无论是在局部极小点还是全局极小点处，我们都有g=0，所以我们就可以通过展开式的第三项黑塞矩阵来判断在该极小点附近的函数长什么样。

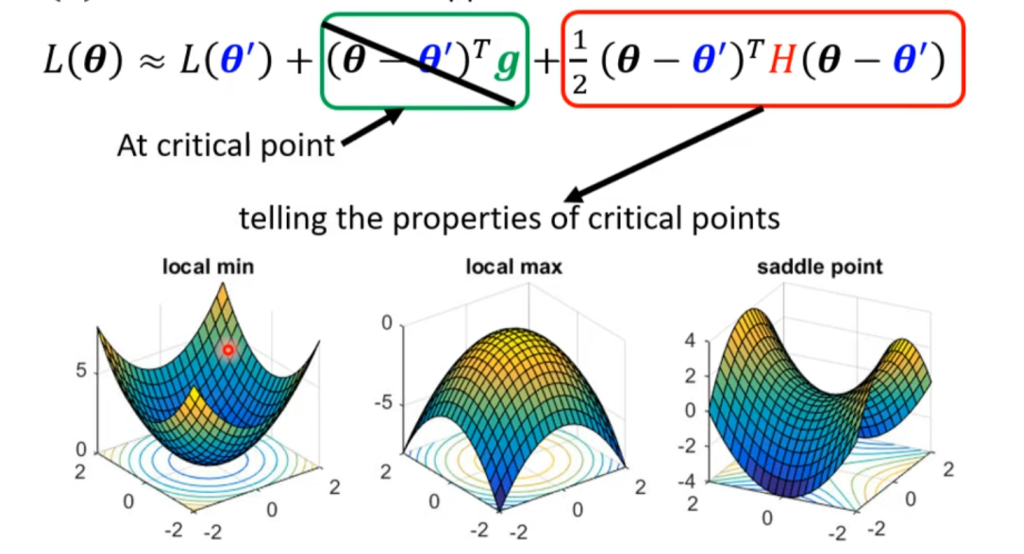
对于local maxima来说，选取任意方向更新都可以下降，但是对于鞍点来说，必须选取下降的方向

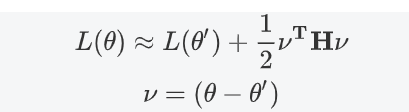
选取为的负特征值为对应的特征向量，所以

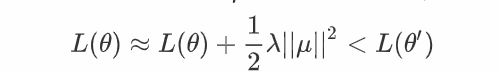
但是这种方法在实际运用中并不常见，因为需要计算出黑塞矩阵，并且要计算特征值和特征向量。

local point 和saddle point哪个更常见？

在实际的机器学习过程中，对于所有的

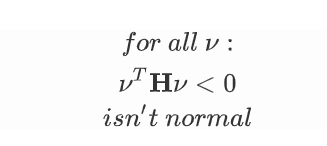
更常见的是一些方向为正，一些方向为负。通常使用minimum ratio来表示

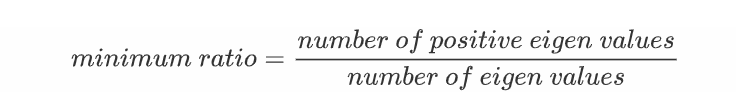
实际常见为小于0.5的值，最大也不过0.5左右，很少出现纯粹的local point

2.训练批次和动量

对于类神经网络的训练过程，我们使用了batch来划分训练数据集，并用每一个batch来计算梯度，更新参数，而不是用所有的训练数据集来更新参数。在这个过程中，对batch的大小的划分同样会影响模型的精度。

如果是使用整个数据集来计算梯度，优点在于能够保证迭代的方向一定是下降的方向，但是缺点是需要计算的数据很大，迭代速度会很慢，并且很有可能卡在局部极小点。

而对于使用batch来划分数据集，迭代参数，由于每一个参数的数据量比较小，所以迭代速度较快，并且由于每个batch的数据均不同，拟合出来的函数也有所不同，所以在迭代过程中不易卡在局部极小点：当前局部极小点在下一个batch数据中可能不是局部极小点，但是同样也有可能错过全局极小点，也就是说划分batch使得迭代不一定朝着下降的方向进行。但是从实际的运用上来看，batch的划分训练出的模型准确度要好于不划分。如下图所示：

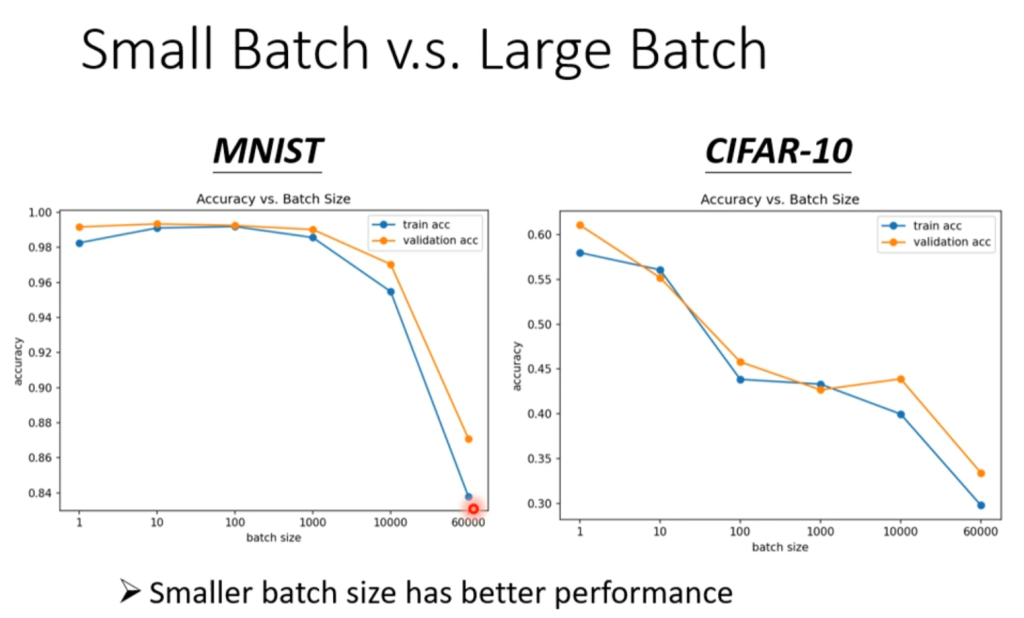
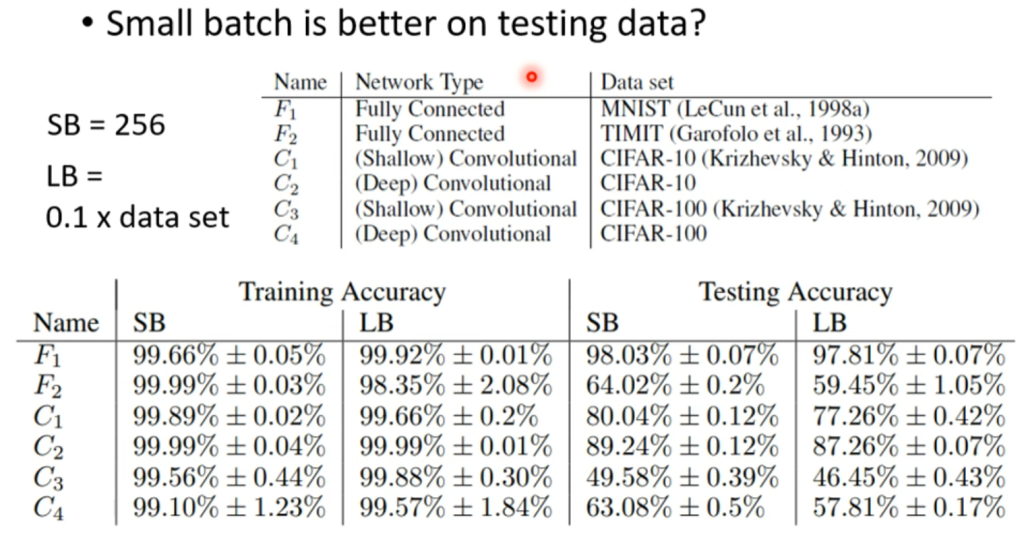
合理划分batch带来的好处还有训练速度上的提升

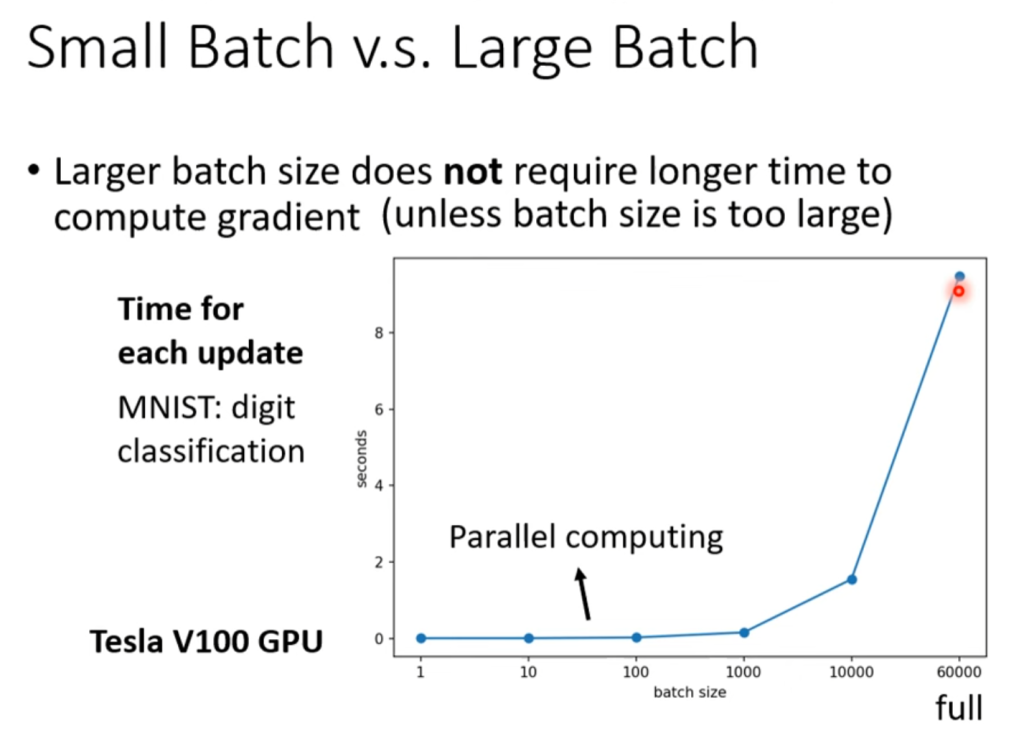
如图所示，batch划分的大小在一定范围内（图中是1-1000）其运算速度是相当的，你可能会认为但是update的次数也随着划分而增加了，但是GPU是可以并行计算的，所以batch的划分可以使得总体的运算速度大大提高，但是也需要注意batch划分不能太低，如本例中如果batch.size=1，那计算次数是60000次，但是如果划分batch.size=1000，计算次数减少为了60次，而单次的运算速度却没有增加多少，使得总体的运算时间大大减小。

动量：在模型的训练过程中，除了使用最常见的梯度下降法之外，还有一种模拟物理重力的下降方法，我们知道物体的运动除了外力的作用之外，还有自身惯性的影响。所以在模型训练的下降过程中，我们为迭代添加”动量”，也就是说下降方向和步长除了受到当前点梯度的影响之外，还受到前一步移动的向量影响，即

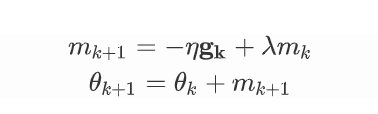
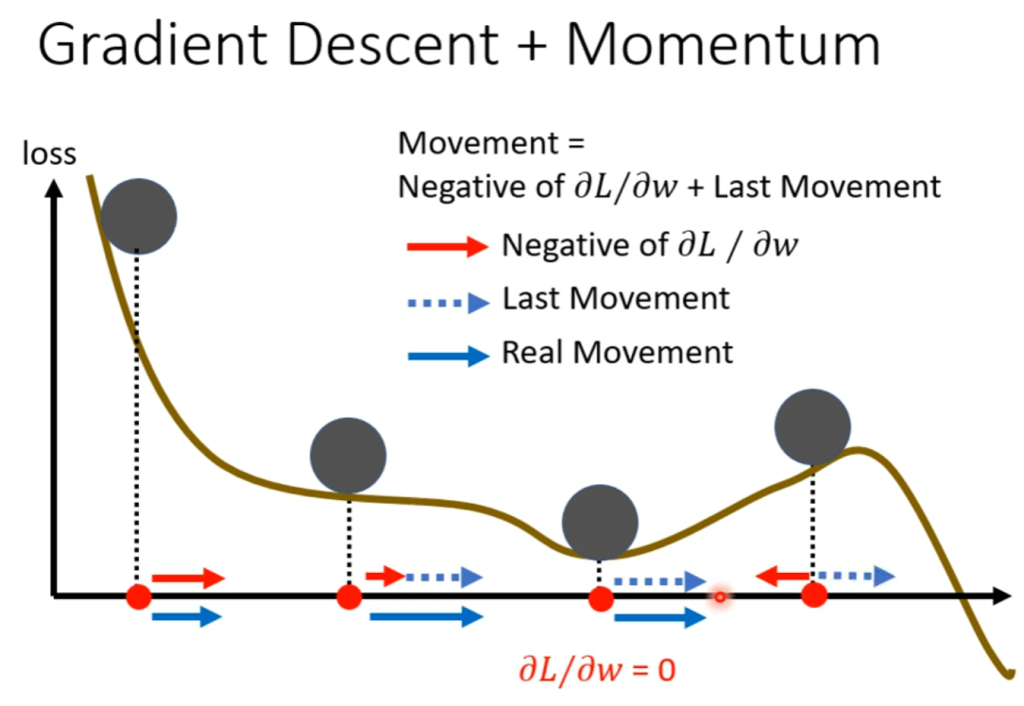
这样，在动量的作用下，模型就有可能跳出当前的局部极小点，然后朝着更优解方向迭代。

3.自动调节学习率

在上一节的最后我们使用动量来修正梯度下降法。现在我们来考虑学习率的问题，在之前的训练中我们一直使用固定的学习率

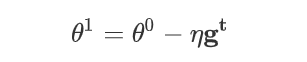
但是这个最基础的模型显然会带来一个问题，就是如果学习率调大了，会在最小点附近的谷底会来回摆动，无法收敛到最小点。如果学习率很小，随着越接近最小点，梯度越小，就导致了移动的步长很小很小，无法靠近最低点。

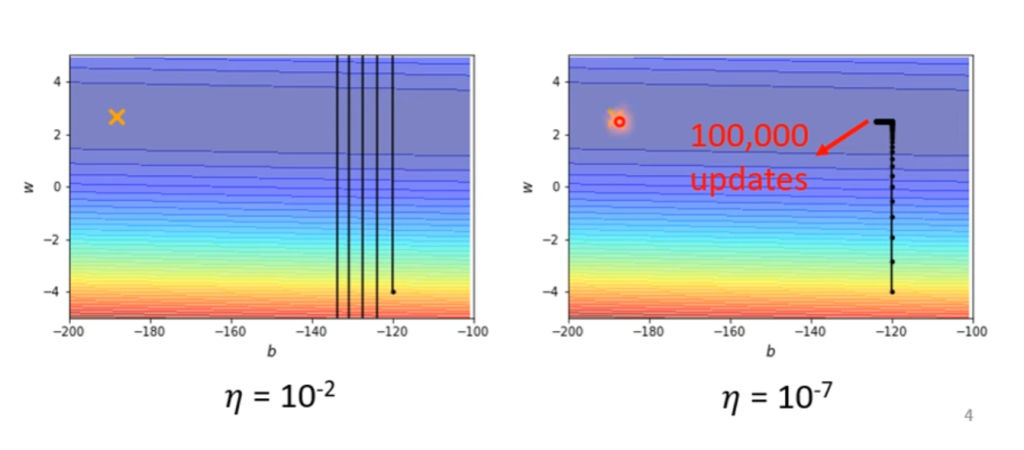
如上图所示，所以我们需要在每次迭代的时候自动调节学习率，使其处于一个合适的范围。问题：为什么没有使用最优化原理中提到的最速下降法？

对于学习率的调整，我们使用RMS（root mean square）方法来调整，具体说来就是：

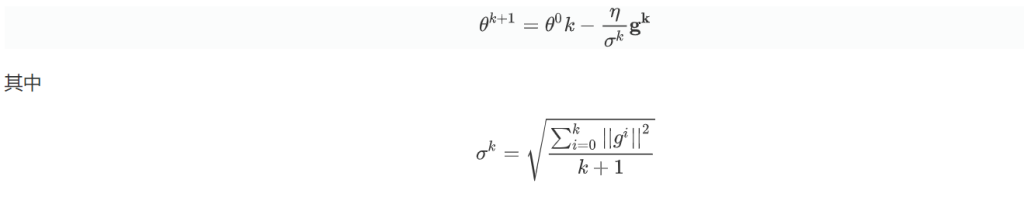
通过这样的调整，当越接近最小点的时候，梯度越小，σ就越小，于是步长就越大，从而实现了稳步接近最小点。

还可以更进一步，通过α调整每次梯度的权重。